by Joseph Pennisi
(see figures and photos below)
Back in the saddle again
I have been retired from engineering for about 10 years, and I finally dug out the old RC stuff. Yep, I have been dragging it around for 40 years or more.
Along with sorting through the old stuff, I have been poring through the current RC magazines. It is incredible how the technology has progressed in four decades. The magazines have changed quite a bit also: less build-it-yourself and more product assessment.
One of the clear advancements is the whole package of electric power systems elements. There are brushless motors, LiPo batteries and electronic speed controls. These gadgets simultaneously bring simplicity and complexity to the hobby. No more fuel tanks, no more needle valves, no more starting motors. But, hold on! There are now amperes, battery capacity, watts and kV to sort out.
I found a biplane (see photo 1) in my pile of stuff that I designed and built in 1972. It seemed like a good candidate for electrical power conversion. I had previously powered it with a .15 glow fuel engine. Now, the question is which motor, battery and ESC to use. The top span is 32 inches, and the flying weight is about 28 ounces.
The most popular approach described in the “rags” and websites was to decide if the plane was to fly 3D, sport or trainer. Then pick a power range (watts) to suit that style of flying. (I must add right here that when I was flying in the 1970s, 3D did not even exist.)
The next step was to pick a motor size (don’t forget to deal with the kV: slow-flyer, moderate speed or speedster), then pick an ESC that would handle the motor current, then pick a battery that would supply the needed voltage and fly the plane long enough to satisfy my “fun quotient.” Oh, by the way, use the largest diameter prop that would fit the airplane. And then try various pitches until satisfied.
This is not a bad approach. I did all of the above and ended up with an electrifly 35-30-950 motor, an electrifly ss-35 ESC and a 3s LiPo battery (20c) with 1500mAh capacity. The system does a really fine job of flying the little bipe, and I have no gooey mess to clean up after each flying session. Great!
There must be a better way
At this point, the engineer in me started to reemerge, and I began to wonder if there was, perhaps, a different (if not a better) way to go about the electric power system design. My thinking was that instead of viewing the prop as the end of the story, maybe it should be at the very beginning of the selection process. After all, this is the device that ultimately provides one of the three basic forces for the aircraft; namely the thrust. The others are, of course, drag and lift.
So how does the propeller create thrust? Well, the blades are twisted (pitched) so they can “cut through the air.” When spun, the prop causes air to move, and that action results in a reaction, which is thrust for the aircraft. The propeller does not care a bit how it gets spun up. You can use fuel, electricity, or steam for that matter. But since we are talking about electrical power systems, let’s proceed along those lines.
Suppose we knew which size prop we wanted to use. Something suitable for the type of aircraft we are building; maybe even sort of scale-like. If we further knew how much thrust we wanted, and how much thrust a prop could provide, we could find a match (diameter and pitch). But wait, we need to spin the prop, and we need to know how fast it should turn to generate the desired thrust. If we knew the requisite rpm, we could find a motor that would provide same, and we are off and running.
Math time (just for a while)
It’s time for some equations. OK; I know some of you are saying I have gone along this far, but this is where I get off the boat. Stick with me, and you will get some insights, even if the math is not interesting to you.
thrust = k1 (x) n squared (x) d to the 4th power
torque = k2 (x) n squared (x) d to the 5th power
Where:
– thrust is the thrust generated by the prop
– torque is the torque required to spin the prop
– k1 and k2 are constants
– n is the rpm of the prop
– d is the diameter of the prop
These equations tell us that thrust and torque are highly dependent on rpm and even more dependent on diameter. This reaffirms the notion that spinning big props fast results in the most go-power.
But what about those constants k1 and k2? I have not been able to find any manufacturer’s data that even hints at this information. So, are the equations useless? Nope! We can figure out the constants ourselves. We run the props at a known rpm and measure the thrust and the torque. Then we solve the equations for the constants, and we are home free. Home free to do what, you ask? You’ll see.
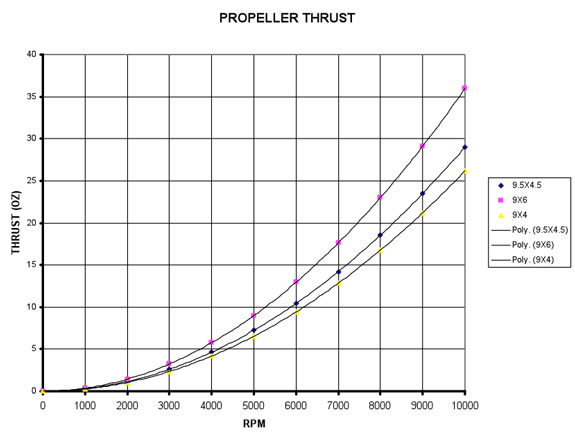
I constructed a homebrew thrust stand (see photo 2) and used an optical tachometer to get rpm. I measured three props; a 9.5-in. diameter by 4.5-in. pitch, a 9×4-in. and a 9×6 in. They were all made of plastic and all made for electric motor use.
The 9.5×4.5-in. prop spinning at 9,500rpm generated 26 oz. of thrust.
k1 = 3.56 x 10 to the minus 11th power
I also ginned up a torque test stand (see photo 3). The torque required to spin this prop at 9,500 rpm was 14 oz.-in.
k2 = 2 x 10 to the minus 12th power
We can now draw curves that characterize the propellers we have tested. These curves allow us to exit the math world (yea!) and simply find points along the prop curves to solve the problem of matching power components to an aircraft.
Let’s get back to the little bipe.
I set a goal that thrust should be about eq
ual to the all-up weight. All three props achieve that goal at rpm between 9,000 and 10,000.
So now we need to find a motor that can deliver the rpm. If we choose a 3s LiPo battery, the voltage is 11.1 volts. The chosen motor carries a kV of 950. This produces an rpm of 10,545 with no load.
For these 9-inch props, the selected motor results in the following rpm, current draw and thrust:
9×6 9,000rpm and 12.4 amp for 29 oz. thrust
9.5×4.5 9500rpm and 9.4 amp for 26 oz. thrust
9×4 10,000rpm and 9.2 amp for 26 oz. thrust
The 9.5-inch prop looks pretty good on the bipe. The thrust is in the ball park, and the current draw is modest.
If only…
If we had two pieces of information from the manufactures, we could have solved the problem going forward instead of going backward. That is,
1. If the propeller folks would give us k1 and k2 (or better yet the curves) for each propeller diameter and pitch
and
2. if the motor folks would give us the torque resulting from a given current
then, the procedure would be as follows…
A. Set the thrust goal
B. Pick a prop size
C. Find the rpm needed to get the thrust (from figure 1)
D. Find the torque required to get the rpm (from figure 2)
E. Find a motor that will provide the rpm for the battery voltage you have picked (kV x voltage)
F. Determine how many amps will be needed to provide the torque (from figure 3)
G. Determine how many minutes you want to fly
H. Calculate the required battery capacity to provide those minutes of flying time
Let’s do an example…
My bipe weighs about 28 ounces; I want to use a 9.5-inch prop. I want to fly about 10 minutes on a charge.
Use figure 1 to find that we need 10,000rpm to get 28 ounces of thrust from the 9.5 x 4.5-in. prop.
Using figure 2, we find the torque required to turn the prop at 10,000rpm is 15.5 oz.-in.
Now we use the motor data (figure 3) and find that a 35- 30- 950
will produce 15.5 oz.-in. of torque at 10.5 amps.
Since battery capacity = amps x time, we can calculate the required capacity as
c = 10.5 amps x 10 minutes = 105 amp minutes or
105 (amp) x 1000(milliamps/amp)/60 (min/hour) = 1,750mAh.
This would be 10 minutes at full throttle. If we say half the flight would be at 1/2 -throttle and half the flight at full throttle, then we calculate
5 x 5 + 5 x 10.5 = 77.5 amp minutes or 1,300mAh
This leads us to select a 1,500mAh battery capacity.
Now, doesn’t that feel good? We have a pretty direct method of sizing the electrical components using engineering principles and data. Ahhh!
One small caution. This approach is based on propeller “static” performance. As the aircraft moves through the air, the parameters change somewhat. Some tweaking may be necessary.






























Excellent job! I am on the same learning curve as you. Makes perfect sense. thanks
I am also an engineer with more than a decade of flying.
One cautionary comment:
The motor also applies an equal one opposite torque to the plane which must be offset by the ailerons.
If you go too big on the prop, the motor will twist the plane into a spin and it will tumble out of the sky, probably out of a turn, for no apparent reason.
That is, of course, that you can take-off without flipping it over.
I figured this out running some awesome looking three bladed props on small WWII scale models.
At somewhat reduced speeds (to conserve battery) in turns, when ailerons would have reduced capability due to less than peak speed and see increased loading due to the turn, they would simply tumble out of the sky!!!
Do not push it!
And if you have a plane crash like that, consider this possibility.
Equal and opposite
Maybe the moderator can correct that?